
Linear Systems in Engineering
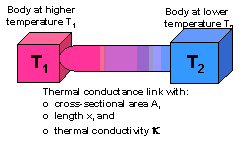
In the discussion of heat transfer by conduction, we identified the behavior of the following simple system:


We also noted that the power transferred (heat flux) between two
points depended on the physical and geometric properties of the
link between them and on the difference in potential (here, temperature)
between the two points. An important consequence of this relation
is that if the system exists in isolation, the potentials (temperatures)
of the two bodies will exponentially approach some midway value
which depends on the relative size (or capacity) of the two bodies
as well as on their initial potentials (temperatures).
Generalization
This linear relationship and the exponential dynamics which results
from it are behaviors which appear much more generally in engineering,
e.g., in gas flow technology, or in electrical circuit behavior.
EquiPSim shows an example from gas flow technology, where the
rate of gas flow through a conductance (e.g., a pipe) is linearly
dependent on the conductance value and the difference between
pressures in the chambers at each end of the conductance element.
In electrical circuits, Ohm's law can be stated that the electrical
current between two points depends linearly on the electrical
conductance between these two points and on the voltage difference
between these points. And in each of these examples, the behavior
will also depend in a similar way on: (1) the relative size (capacity)
of the two points; (2) the initial values of the two points; (3)
the geometric dimensions of the link between them; and (4) the
material properties of the link between them.
Mathematical representation
We can represent the general behavior as:
Flux
= conductance x potential
difference
|
|
|
|
|
| Molecular flow of gases | Gas flow | Vacuum conductance | Pressure difference |
| Conductive heat transfer | Heat flow (power) | Thermal conductance | Temperature difference |
| Electricity | Electrical current | Electrical conductance | Voltage difference |